在实际工程和科学领域中钝体绕流具有广泛的研究意义。工程应用方面涉及海洋石油平台、柔性深海立管、桥墩柱、高空电缆等。科学研究方面包含有尾流、自由剪切层、边界层、旋涡脱落和涡动力学等，这些都是全面理解流体动力学的基础，并且应用于广泛的工程实践。为了进一步理解流体动力学的物理机理，大量的学者就钝体结构的三维不稳定性展开了大量的研究，并结合各种方法，包括有实体物理模型试验[1,2]，直接数值模拟[3]和线性稳定分析等方法[4]。

绕流研究中，圆柱绕流是最为经典的课题，大量学者对其进行了广泛的研究，其三维转捩过程主要经历了以下几个阶段:三维不稳定模态首次出现于雷诺数约为190时，此模态被定义为模态A，其展向波长约为4D(D为圆柱的直径，即钝体的特征长度)。随雷诺数增大，大尺度涡模态A*开始产生和发展。当雷诺数达到约230时，不稳定模态B出现，其展向波长表现为0.8D肋状涡旋。当雷诺数超过270后，模态B的发展愈加无序，流场向湍流发展。方柱也为典型的钝体形式，方柱绕流的两个基本不稳定模态发展研究的物理机理与圆柱具有一致性。其差异性表现在，方柱产生的模态A的展向波长约为5D，模态B的展向波长约为1D，均略高于圆柱。且三维不稳定模态A和B出现于比圆柱更早的Re=165和Re=185。

此外，一种具有双周期特征的不稳定模态C在靠近单圆柱的细线的研究中由Zhang[5]首次发现并提出。模态C的结构特征与模态A和B具有显著的差异。

当钝体结构为不同的形式，数量和排列时，在尾流不稳定模态转捩的研究中发现一些新的演化过程和流体机理。近年来，对多样化的钝体结构形式进行了较多的探索。等距布置的四圆柱有较多学者进行了研究，Lam[6,7,8,9]早期研究了根据不同的间距比所产生的尾流特点并分类为3种流型，之后通过三维数值模拟研究了在雷诺数为200时，不同的间距比和长宽比对三维流特性的作用。Lama[10]总结了在临界雷诺数下不同间距比对水动力系数和压力分布的影响。Tong[11]总结了间距比为2，不同雷诺数的旋涡脱落规律和四圆柱的流体动力特性，并根据不同的雷诺数区间将尾涡结构分为4种流态。

三维效应下，流场中的多模态共存和相互作用十分复杂，采用直接数值模拟能够有效的捕捉三维涡结构并进一步分析流动机理。

本文将对等边布置四方柱的三维不稳定性的尾涡发展的全过程进行研究。直接数值模拟采用高阶谱单元方法对均匀流下的纳维-斯托克斯方程(N-Sequation)进行求解。四方柱间距比为2.5，雷诺数范围从150到300。结合水动力系数、流型、能量曲线、尾涡结构等方面分析不同雷诺数下三维不稳定性的发展过程。

1、数值模型

1.1计算方法

三维粘性不可压缩流的Navier-Stokes

方程如下:

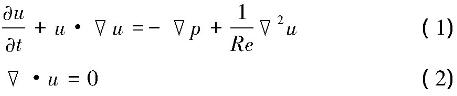
式中u、t、p、Re分别为速度矢量、时间、压力和雷诺数。其中Re=U∞D/υ，U∞为自由来流的匀速度，D为钝体的特征长度，υ为运动粘度。

本文采用嵌入开源代码Nektar++的谱单元法求解N-S方程。基于流动变量在展向是均匀的假设。在z方向上对流动变量u和p进行傅里叶展开:

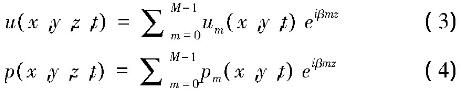
式中m是傅里叶模态指数，M是模态数。其中β=2π/Lz,Lz为周期长度。将方程(1)(2)进行傅里叶变换，各模态的二维解耦方程如下:

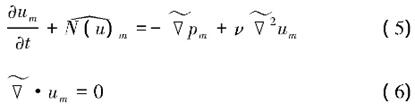
式中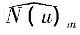为傅里叶模态的对流项。算法的详细内容见Karniadakis[12,13]的研究。

1.2计算模型

四方柱的计算域如图1所示，坐标系的原点取在4个方柱的中心，4个方柱的尺寸完全一致，边长定义为D,2个方柱的中心距定义为L。上下游边界距离原点分别为32D和52D，上下侧边界距离原点均为32D，模型展向高度取8D。本文研究的方柱间距比L/D为2.5。本文边界条件设置为在入口边界和2个侧边界采用均匀流速(u=1,v=0)，出口边界采用Neumann边界条件。方柱表面设置无滑移边界条件(u=0,v=0)。四方柱的网格划分如图2所示，整个计算域采用结构化网格，在靠近方柱周围网格进行加密处理。

图1四方柱计算域

图2四方柱网格划分示意图

1.3数值验证

为了验证本文所采用的数值方法及参数的准确性，选用单方柱进行数值计算。相关的水动力系数:阻力系数CD、升力系数CL和斯特劳哈尔数St，定义如下:

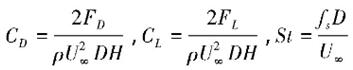
式中，FD为阻力，FL为升力，fs为脱涡频率，H为z方向高度。

通过与其他文献的平均阻力系数、均方根升力系数C'L和斯特劳哈尔数St进行比较来验证。考虑到本文研究的是三维不稳定模态的发展，所以选用单方柱开始进入湍流的Re=300作为验证算例。表1列举了多项式阶P=8的算例与其他学者研究所得数据的对比。C'L和St值与之前的研究吻合较好，而值略高是由于不同的研究方法及模拟条件，包括边界条件、阻塞率、网格疏密等方面的差异。单方柱绕流的数值模拟结果表明Nektar++对低雷诺数下的数值解具有可靠的精度。

表1Re=300，单方柱绕流计算结果

此外，通过改变多项式阶数P，对所讨论的物理模型进行精度的研究，选用Re=200和L/D=2.5作为网格独立性分析的验证算例。表2列举了4个不同的多项式阶(P=6,7,8,9)的上游方柱1的水动力系数结果。分析表明，当P≥8时相对误差已经小于1%。综合考虑计算效率，本文采用P=8的多项式阶作为研究离散化解的精度。

表2Re=200,L/D=2.5，四方柱绕流上游方柱1的计算结果

2、计算结果与分析

2.1雷诺数对升、阻力系数的影响

上下游4个方柱的平均阻力系数CD-和均方根升力系数C'L随雷诺数的变化如图3,4。每个数值结果均取用了至少500个无量纲时间，以保证准确度。图中对照组采用了Jiang[16]的单方柱算例和Tong[11]的四圆柱算例结果。本文研究的4个方柱的数值结果均在图中绘出。四圆柱在中等间距比下，表现为上下对称的2个平行串列圆柱，且2个上游圆柱和2个下游圆柱的水动力特性值具有高度一致性。但对于四方柱，来流分离点均发生在尖角处，以及上下游钝体间的尾流互扰等因素，导致上游两方柱和下游两方柱在一些特定雷诺数下，升阻力系数具有一定差异性。

图3平均阻力系数随雷诺数变化折线图

图4均方根升力系数随雷诺数变化折线图

如图3所示，随雷诺数的增大，上游方柱1和方柱2的值基本呈上升趋势，但增幅很小。下游方柱3和方柱4的值则有一定波动。在Re≤200时，上游方柱1,2间和下游方柱3,4间的值完全相同。当雷诺数超过200后，值开始出现差异，其中在Re=250时，上游方柱1和方柱2的值的差异较明显，对应的上下两侧尾涡结构演化出较为特殊的模式，下一节具体分析。其中在Re=250和Re=275时，下游方柱的值出现负值，这2个阶段的稳定流型均表现为同相位流态。与四圆柱进行比较可以看出，下游圆柱和方柱的值相差不大，因为间距比较小，上游钝体阻挡了来流，导致来流对下游钝体作用减小。而上游圆柱和方柱的值有较大差距，通常方柱力系数在相同雷诺数下均比圆柱要大，主要由于方柱的结构形式迫使来流在前角就开始发生分离。四方柱的值也比单方柱大，主要是因为中等间距下的上下两侧流场间的相互干扰。

如图4所示，下游方柱的C'L值远大于上游方柱，是因为下游方柱的尾部旋涡发生脱落。在Re≤200时，上游方柱1,2间和下游方柱3,4间的C'L值也完全相同。随雷诺数增长，C'L值也开始产生差异。在Re=250时，上游方柱间和下游方柱间的C'L数值相差较大，上游方柱1比上游方柱2的C'L值高31%，下游方柱4比下游方柱3高18%。从图中可以看出，随雷诺数的增加，圆柱的C'L值不断递增，方柱的C'L值在雷诺数增长早期也单调上升。但在Re=225～250,C'L值发生骤减，在此雷诺数范围下对应的尾流正处于转捩阶段，从反相位流型转变为同相位，其中尾涡展向结构也发生变化，这将在2.2和2.3节具体分析。

2.2瞬态流型和力系数时程曲线

二维瞬时展向涡量图取自三维展向涡结构中心截面。当间距比L/D=2.5时，上游方柱后的旋涡尚未脱落，在本文研究的雷诺数150～300区间下，上游方柱后尾流均表现为剪切层再附着状态。当Re=150时，三维不稳定性还没有出现，流型由初始阶段的同步反相位转变为同步正相位模式。随着雷诺数增加，三维不稳定性产生，在Re=175和Re=200下，如图5(a,b)所示，流型均表现为同步反相位模式，且都处于周期层流态，尚未进入尾迹转捩阶段。

图5中间平面瞬时展向涡量图

如图6所示，当Re=225时，流型经过早期的同步反相位模式后，很快在远尾迹处出现扰动，尾流表现出非对称和不稳定的特性，尾流已经进入转捩阶段。升阻力系数的时程曲线具有一定的周期性。如图6(d-h)t=1600～2000的中心截面的瞬时展向涡量图所示，近尾流流型多表现为反相位，且尾迹发展也主要为反相位特性，但上下两侧涡街的涡脱落频率存在差异，同时涡街呈现向上下侧摆动的特点。在t=1900时，近尾流表现为同相位模式，但远尾流无序破碎。在雷诺数为225时，反相位模式虽占据主导，但尾流发展不稳定。

当雷诺数增加到250时，由图7(a,b)可以看出，在t≤900左右，升阻力时程曲线的振荡周期和幅值和Re=225时比较接近，且展向涡量图的流型特征也很相似，但近尾流处流型基本上均表现为同相位模式。随着尾涡继续发展，当t≥1300左右，升阻力时程曲线趋于平稳，幅值保持不变，说明流态发展充分，尾流流型均表现为同相位模式。雷诺数进一步增长至275(图5(c))，流型仍保持为同相位模式，时程曲线很快趋于平稳，流态较早的趋于稳定。当雷诺数到达300时(图5(d))，近尾流旋涡发展无序，向下游运动的旋涡已经十分紊乱，且尾流场中出现许多破碎的小漩涡，湍流特性明显增强。

2.3三维不稳定模态分析

尾涡结构的展向波长是研究产生三维不稳定性流体性质的重要指标，通过能量曲线和三维涡结构来分析主导模态及各模态间的相互作用。本文选用32个傅里叶模态确保准确的捕捉各雷诺数下沿展向尾涡结构的变化。为了定量研究三维流的发展和各尾流模态间的相互作用，动能随时间发展的公式定义如下:

图6Re=225，升阻力时程曲线和不同时刻处中心平面瞬时展向涡量图

图7Re=250，升阻力时程曲线和不同时刻处中心平面瞬时展向涡量图

式中k为展向波数，V为计算域的体积。

图8Re=150，三维展向涡等值面ωz

当雷诺数为150时，能量曲线快速衰退，四方柱尾流场未出现三维效应，该工况下处于二维层流阶段，图8表示Re=150时四方柱展向尾涡的三维结构，表现为两组相反符号的蓝色面和红色面的旋涡交替排列，具有冯卡门涡街的典型特征。该等值面充分反映了尾流和旋涡脱落的二维本质，其在展向表现为均匀性和光滑性。

图9模态能量的时间序列和可视化三维涡结构。流向涡用正负的红蓝实体表示，展向涡用灰色半透明体表示

随着雷诺数增加至175时，三维不稳定性已经产生。如图9所示，在尾涡的初始发展阶段，各波数模态的能量值先快速下降，再以指数速率快速上升。能量曲线中不稳定波数5模态达到饱和峰值，并占据主导，波数5所在能量组的其他谐波的能量值均达到峰值且趋于稳定，而其他组的能量值不断下降。图中的三维涡结构表现为有序且沿中心线对称的波浪形展向涡旋和肋形的流向涡旋。主导波数5模态完全对应于沿展向的5个周期的流向涡对，其相应的展向波长为1.6D(D为方柱的边长)。如图9(a)所示，雷诺数为200时，对应的主导能量模态及三维涡旋与Re=175时高度一致。说明雷诺数在175～200范围内均由相同的模态主导。

前文指出在Re=225时，尾流进入转捩阶段，流型发展不稳定，升阻力曲线表现出周期性振荡。能量曲线也表现出同样的周期性波动(图10)。在t=100左右，波数5处于各波数模态能量值中的最高值。三维涡结构沿展向的流向涡对也为5个周期，见图10(b)。在t=100左右，波数5处于各波数模态能量值中的最高值。到t=200时，波数1达到一个峰值点，从图10(c)中可以看到，近尾流处仍为4个涡对，但在下游发展的远尾流处为沿展向1个周期的大尺度涡对。由于Re=225的能量曲线随时间非线性增长，这种非线性效应促使各波数涡旋共存并相互作用，进而产生更小波数的流向涡结构。但随着尾涡继续发展，波数1和5很快被波数4取代，波数1和5的能量值不断衰退，而波数4及其谐波组成为主导模态组，对应的三维涡结构的流向涡对沿展向为4个周期。如图10(d)所示，波数5及其谐波的能量曲线出现周期性波动，对应说明了此雷诺数下尾涡流型处于不稳定阶段，流向和展向涡结构失去了Re=175～200阶段有序的对称性。

雷诺数进一步提高至250时，由图11的模态能量的时程曲线看出，在尾涡发展的前期，多个模态能量竞争剧烈，对应多个波数的三维涡旋相互作用。t<1000的阶段下，不稳定波数1模态占主导作用，但通过可视化三维涡结构并没有看到主导波数1的存在，这是因为多个波数模态共同作用，且均获得了较高的能量值，三维涡旋中多个不稳定波数模态共存，所以将流场涡旋识别为一个周期的波数模态。当t>1000后，经过了约200多个时间单位的过渡后，各不稳定波数模态能量值趋于稳定，表示三维涡旋结构进入稳态。通常三维涡结构的展向涡对周期在上下两排应为一致，但Re=250的工况下，上排方柱1和4后的流向涡对数以波数4模态主导，而下排方柱2和3后的流向涡对数则以波数5模态主导。其现象背后的流体机理暂不明确，后续将进一步研究。

图10(a)Re=225时模态能量的时间序列。(b～d)可视化三维涡结构

前文分析指出，当Re=250～275，流态虽处于尾迹转捩阶段，但主涡核的平面瞬态流型表现为同相位模式。如图12所示，Re=275的尾涡发展初期多个波数模态共存并相互作用，致使波数1为主导模态。当尾涡充分发展后，波数模态4及其谐波的能量值达到饱和趋于平稳，此后波数4为主导模态，相应的展向波长为2D。可视化三维涡结构沿着展向也表现为有序的4个流向涡对。

对于间距比L/D=2.5，尾涡的展向波长均在1.6～2D的范围内，具有中等展向波长的特征，这与第3种基本不稳定性modeC非常相似，由图13流向涡量图可以看出。并且满足modeC的2倍于涡旋脱落周期的双周期特性。不论是从不稳定波数的能量曲线还是从可视化三维涡结构的角度来看，均说明三维不稳定性modeC占据绝对主导。

当雷诺数到达300后，全部波数模态均达到较高能量值，能量曲线表现为不规则的振荡(图14)，可视化三维涡结构开始向无序发展，远尾迹涡出现破碎，流态开始向湍流进展。

从流型和不稳定波数的方面来看，对比于Re=175～200阶段，波数5模态占据主导，且对应的尾流流型为反相位模式。当Re≥250后，主导波数模态为4时，对应的尾流流型表现为同相位模式。说明随着雷诺数的提高，自三维效应的出现，流型从反相位模式逐渐转变为同相位模式，不稳定波数模态由波数5主导过渡为波数4主导，且2个主导波数模态均属于第3种不稳定性ModeC。

图12Re=275时模态能量的时间序列和可视化三维涡结构

图13Re=175～275，中心平面瞬时流向涡量图

3、结论

本文雷诺数选用了从150～300的7个工况，采用了高精度谱单元法对间距比L/D=2.5的方形布置四方柱进行直接数值模拟，通过升阻力系数随雷诺数的变化规律，瞬态流型，能量曲线和可视化三维涡旋来研究和分析四方柱在均匀来流下的三维不稳定性发展特性。

图14Re=300时模态能量的时间序列和可视化三维涡结构

在雷诺数为150时，四方柱的三维不稳定性还没有产生，流态还处于二维周期层流态。随着雷诺数进一步提高，当Re=175～200阶段，尾涡的平面瞬态展向涡量图所表现出的均为有序对称的同步反相位流型，升阻力时程曲线发展平稳，且上游方柱间和下游方柱间的和C'L值完全相同。能量曲线中的主导波数模态均为波数5，对应展向波长均为1.6D。

当Re=225时，升阻力时程曲线出现周期性波动，瞬态流型在四方柱的近尾流处出现反相位模式和同相位模式间的切换，但反相位模式仍起控制作用。能量曲线中不稳定波数4在尾涡充分发展后起主导作用，对应的展向波长为2D。雷诺数提高至250时，各波数模态在尾涡发展前期相互作用强烈，之后能量值趋于平稳，表现为不稳定波数4主导，且瞬态流型为同相位模式，但可视化三维涡结构中出现上下侧流向涡对数的不同，上游方柱间和下游方柱间的和C'L值产生较大差异。从雷诺数225到250,C'L值出现骤减，说明流态正处于尾流转捩阶段。当Re=275时，流型表现为同相位模式，不稳定波数4占主导。雷诺数进一步提高至300，有序涡结构开始破碎，湍流特性增强。

本文研究的L/D=2.5在各雷诺数下产生的三维不稳定性均为modeC，并没有出现任何modeA和modeB的特征，说明四方柱在L/D=2.5蕴含特有的流体特性。

张宇航,王锐,韩兆龙,周岱,包艳.四方柱绕流的三维不稳定模态发展[J].科技通报,2020,36(06):1-9.

基金:国家自然科学基金资助项目(11772193,51679139,51879160);上海市自然科学基金(18ZR1418000,17ZR1415100)资助;上海交通大学新引进人员科研启动基金(WF220401005);上海高校特聘教授(东方学者)岗位计划;上海市国际科技合作基金项目(18290710600).